Use Mapping Notation to Describe a Translation Up 8 Units.
Now there are other ways that you could describe this translation. 5 units to the right 4 units down.
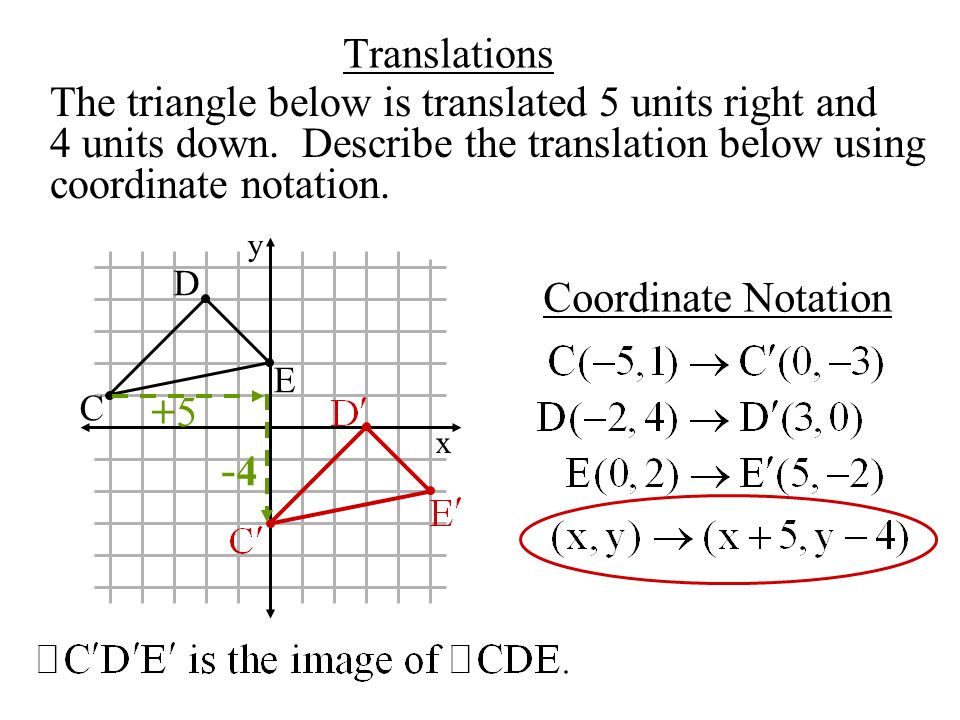
Translations Mathematics Quizizz
C In words describe what the rule is asking you to do.
. In the animation below you can see how we actually translate the point by 1 in the x direction and then by 2 in the y direction. Translation A translation moves a shape up down or from side to side but it does not change its appearance in any other way. The figure shows the parabola y x 2 with a translation 5 units up and a translation 7 units down.
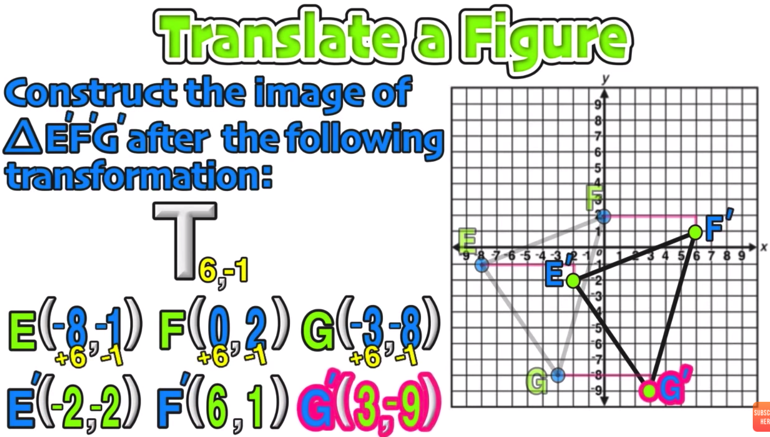
1a3 and 5b1 a4 b6 The rule is. Were gonna go one two three four five units to the left and then were gonna go three units up. X y x 6 y 2 6 units to the right 2 units down Describe the translation as an ordered pair.
X y -- x-20 y10. E Identify the coordinates of Δ. There are two main ways to do this.
Where do you end. X y xa yb. B Describe how the graphs of y- 2 x2 and y x - 52 compare to the.
Fx x2 fx 3x 82 5 gx gx 4 𝑥 6. Identify a translation and use coordinate notation to write correctly see example 2 page 422 Use Theorem 75 page 421-422 see example 1 on composition of reflections Perform a translation given the coordinate notation. You start at 1 0.
Graph of a function up down left or right. The first is through function mapping notation. Each point shifts a units horizontally and b units vertically.
26 3 Use mapping notation to describe how the graph of each function can be found from the graph of the function y f x a y f x b y f x c x f 4 Determine the zeros of the function 43 f x x x after each transformation. If a is negative the function moves left and if b is negative the function moves down. Xyrightarrow xayb is a translation of a units to the right and b units up.
You move up 3 units and right 2 units. A transformation is a way. T U V f Using the image of Δ.
And so the image of point P I guess would show up right over here after this translation described this way. So thats going to be one two three. X y ---- x a y b where a and b are constants.
A y f x b y f x 5 The graph of a function y f x is. Translations in a coordinate plane can be described by the following coordinate notation. X yx 5 y 4 Describe the translation in words.
Find the horizontal change and the vertical change for the translation P4-4 -47 A. The transformations are performed in order from right to left. Shana translates building c to the location of building E use mapping notation to describe the translation of building c Shana translates building c to the location of building E use mapping notation to describe the translation of building c.
So we start right over here. Xy xy8 C. 72 Reflections Identify a reflection and the line of reflection.
Horizontal translation right by 2 units. X y -- x0 y5-This represents a. Describe the translation in the coordinate plane shown below.
Use mapping notation to describe a translation up 8 units. As the animation shows a translation of T 1 2 on the point A with coordinates 3 2. B The parent function is gx The parent function has been vertically stretched by a factor of 4 reflected in the y-axis horizontally compressed by a factor of translated 4 units to the left and 6 units up.
Xy x 8 y-8 B. And we can describe how the 2 graphs compare mathematically using what we call mapping notation y x2 3 y x2 x y NOTICE. Translations are often referred to as slides.
X y -- x2 y0-This represents a. The point cxy is reflected over the x-axis. Fx fx-ab In this case the function moves a units to the right and b units up.
Of 3 translated 8 units to the left and 5 units down. Sliding up or down. Each yvalue had 3 added to it.
Y - 10 fx 20-Mapping notation. Using the rule x y x 3 y - 3. Alternatively a translation can be denoted.
Learn to use notation to describe mapping rulesand graph images given preimage and translation. We can describe how the 2 graphs compare verbally. Graph Translations of the Form y- k fx and y fx-h a Graph the functions y 2x2 y - 2 x and y x - 52 on the same set of coordinate axes.
TUV perform an additional translation. Y fx - 2-Mapping notation. Both numbers tell us about how far and in what direction we are going to slide the point.
Translation Notation Graphical introduction to image translations. A translation is a type of transformation that moves each point in a figure the same distance in the same direction. _____ d Draw the image Δ.
Describe the translation as an ordered pair. Write the mapping rule to describe this translation for Mikah. State the new coordinates of Δ.
Recall the following notation for translations reflections and rotations. A translation is a slide which means that the function has the same shape graphically but the graph of the function slides up or down or slides left or right to a different position on the coordinate plane. Xy x8 y8 D.
In geometry a transformation is an operation that moves flips or changes a shape called the preimage to create a new shape called the image. Mikah describes a translation as point D in a diagram moving from D15 to D31. Using the rule x y x - 3 y - 1.
In this case D15D1a5b or D15D31 Therefore. A parabola is the graph of a second. A translation occurs when the location of a graph changes but not its shape or orientation.
Vertical translation up by 5 units. Xy x8 y.

Use Mapping Notation To Describe A Translation Up 8 Units Brainly Com

Geometry Translations Explained Examples And Extra Practice Mashup Math
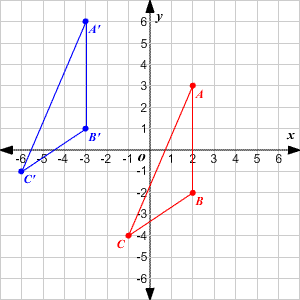
Comments
Post a Comment